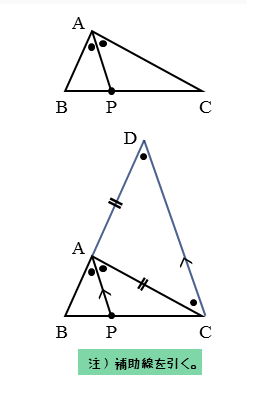
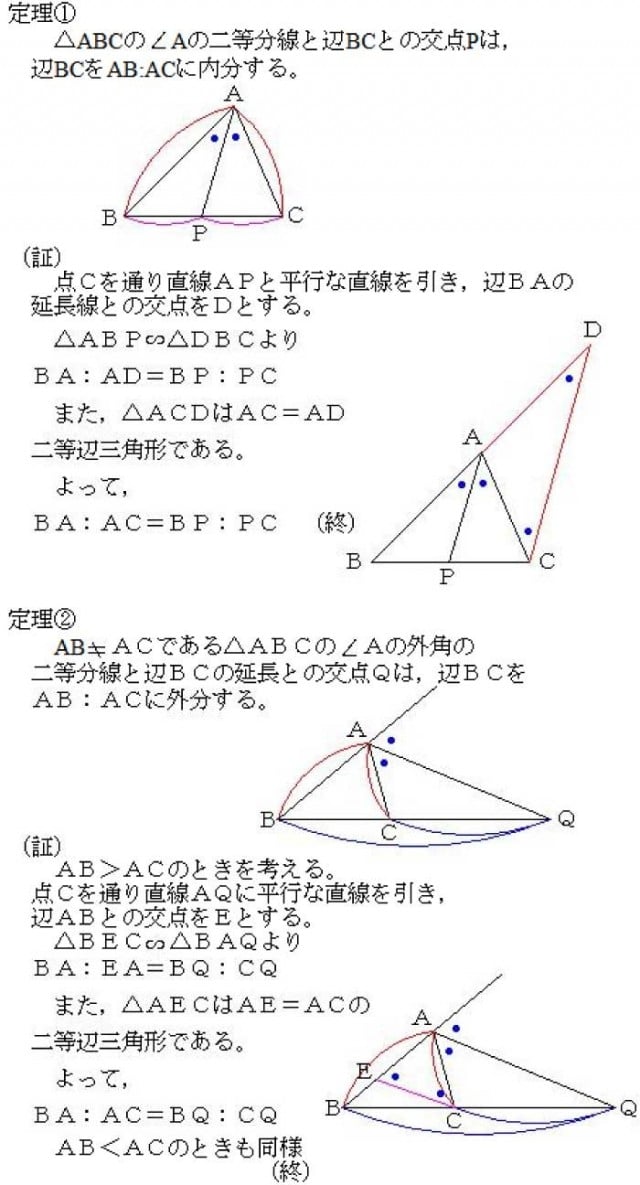
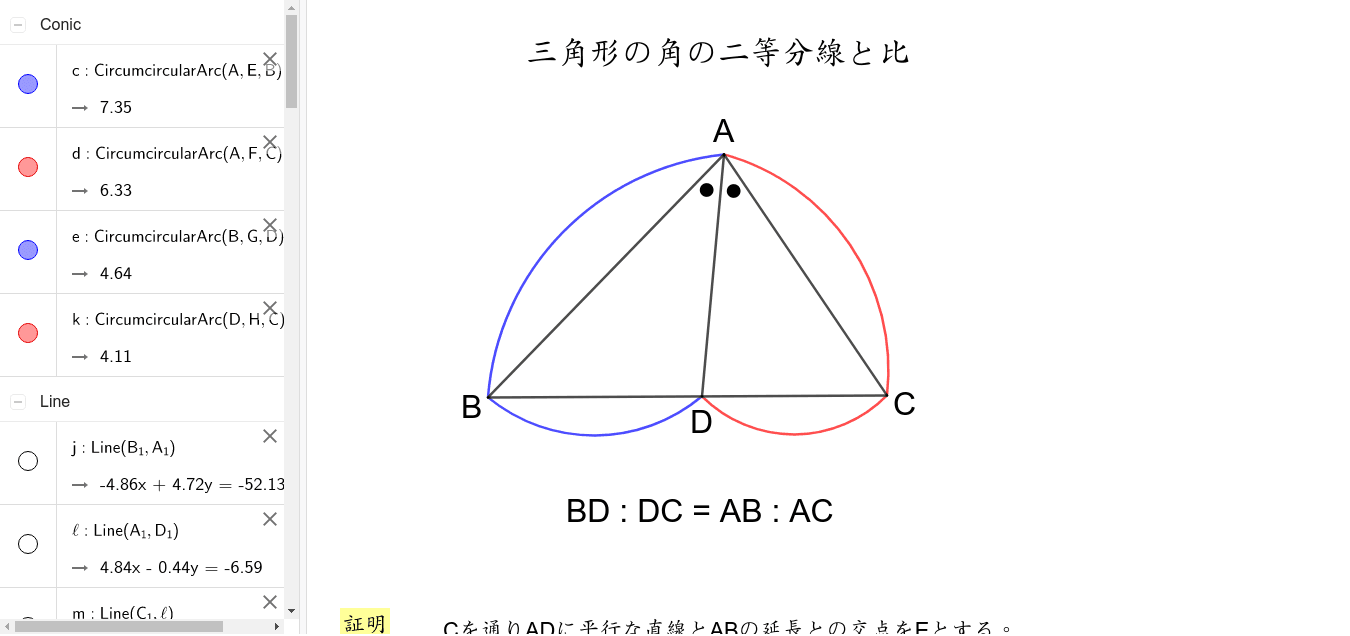
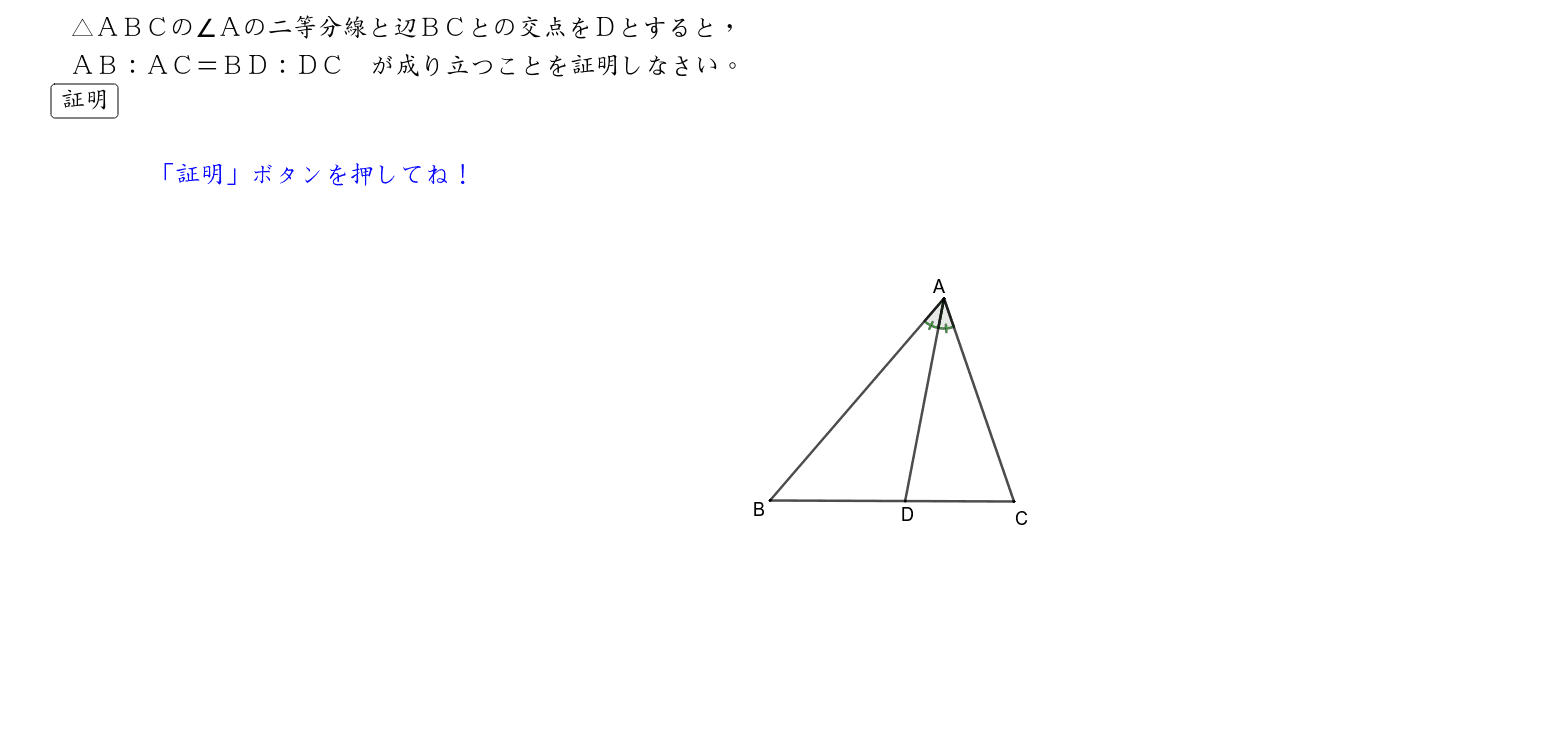
角の二等分線のベクトルは,\ 2つの方法で求めることができる\ どちらも重要である $$角の二等分線と辺の比の関係} (数A:平面図形)}を利用する { $$}$∠ {AOB}の二等分線と辺 {AB}との交点を {C}とする$ ひし形の対角線が内角を二等分することを利用する三角形の角の二等分線と比 三角形の内角の二等分線と比 a bc の∠a の二等分線と点bc との交点d は,辺bc をab :ac に内分する。 すなわち bd :dc =ab:ac 証明 点c を通りad と平行な直線と直線ab の交点をe とすると, a d / / e c より,Ð =Ðca d a cb ,Ð =Ðba d a e cFdData 中間期末:中学数学3 年:平行線 三角形と線分の比/平行線にはさまれた線分の比/平行線と線分比応用/ 三角形の角の二等分線と線分の比 /中点連結定理:証明問題/長さ・角度の計算/全般/ FdData 中間期末製品版のご案内

中3 19 1三角形の角の二等分線と線分比 Youtube
三角形の角の二等分線と比 問題
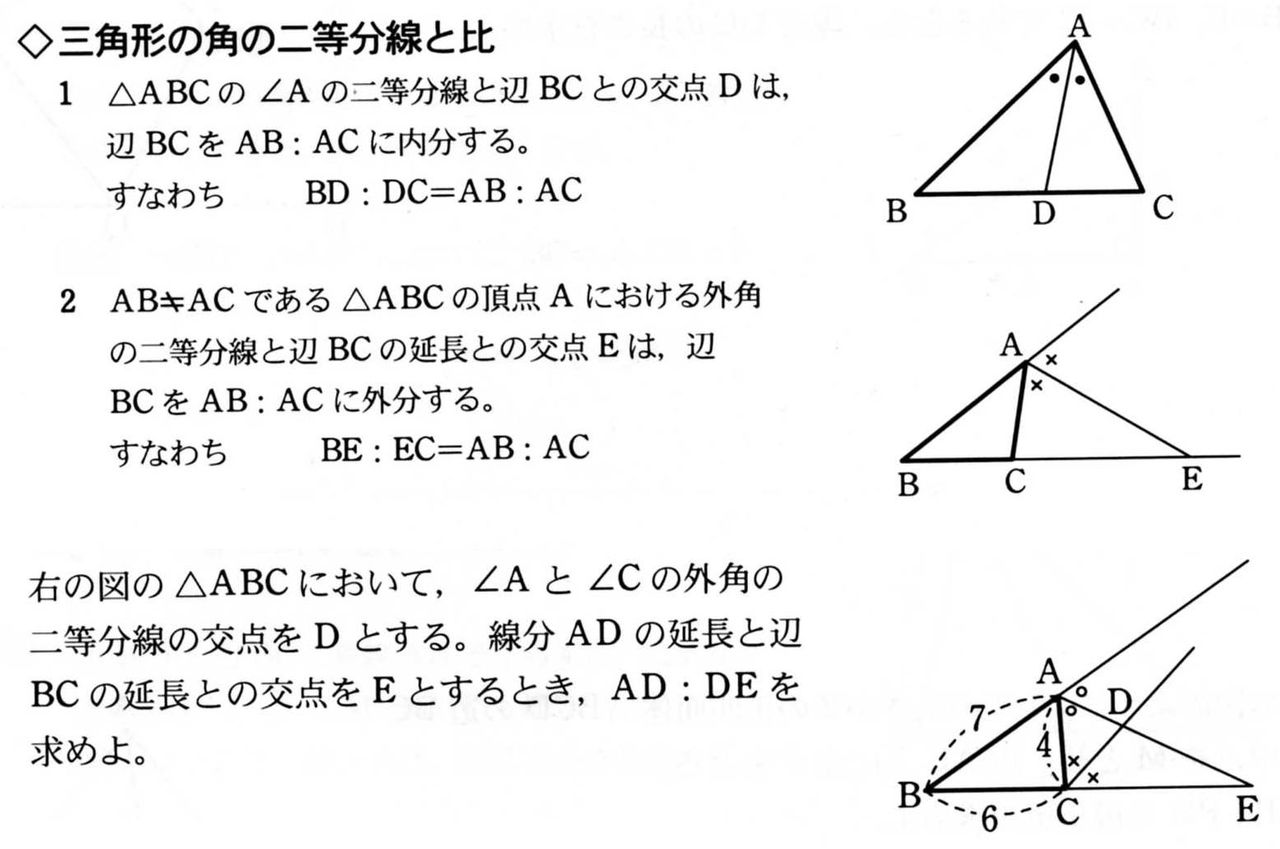
三角形の角の二等分線と比 問題- 三角形のひとつの角の二等分線が与えられたとき,次の基本的な比の関係式が成り立ちます. 三角形の内角の二等分線と比: △ ABC △ A B C の ∠A ∠ A の内角の二等分線と辺 BC B C との交点を D D とする.このとき,次の関係式が成り立つ. 角の二等分線を引くと次のようになる。 AD の長さを求めるために,ADを含む三角形を探すと A B D と A C D が見つかる。 A B C の面積を求めることができることを利用して,ADの長さを求めよう。 A B C = A B D A C D 1 2 AB ∙ AC sin 1 ° = 1 2 AB ∙ AD sin 60 ° 1 2 AC ∙



図形の性質 角の二等分線と比について 日々是鍛錬 ひびこれたんれん
(三角形の角の二等分線に関する公式2) (証明) CからADに平行な直線を引き、Abとの交点をEとする。 よって、 ACEは二等辺三角形、AE=AC。 ADとECが平行より、AB:AE=BD:DC、 AE=ACだから、AB:AC=BD:DC。 三角比と角の二等分線 角の二等分線とは、角を同じ大きさに分ける線のことです。下の図で言うと、 AD が $\angle \mathrm{ A }$ の二等分線です。 有名な性質として、 $\mathrm{ AB }\mathrm{ AC }=\mathrm{ BD }\mathrm{ CD }$ になる、というものがあります。 次のように、 C を通り、 AD に平行な線をひくと 三角形の内角・外角の二等分線と辺の比の関係とその証明 三角形の角の二等分線と辺の比Aの二等分線と辺BCの交点P}}は,\ 辺BCを\ \syoumei\ \ 直線APに平行な直線を点Cを通るように引き,\ 直線ABの交点をDとする (右図) (同位角), (錯角)}$ \\ 2zh \phantom { (1)}\ \ 仮定
三角比からみた角の二等分線の性質 市立札幌旭丘高等学校 中村文則 三角形abcの内角aの二等分線と辺bcとの交点をdとすると, abac bd dc が成り立つ 角の二等分線の性質は幾何の有名定理のように数学者の名前で呼ばれる定理ではないが,三角形の種々の性質この頁では,角の二等分線を題材にして,補助線の引き方を練習します. 図1 角の二等分線の性質 ABC において右図2のように線分 AD が∠ A を二等分しているとき, BDDC=BAAC が成り立ちます. ※この定理は中学校では習いませんので,中学生に対し内角の二等分線と辺の比 三角形abcにおいて、角aの内角の二等分線とbcとの交点をDとすると、ab ac = bd dc が成り立ちます。 証明は、cを通りDに平行な直線を引いて、相似三角形を作ります。
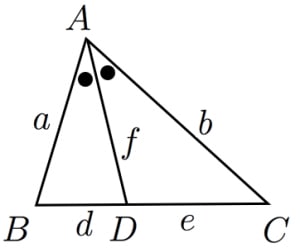
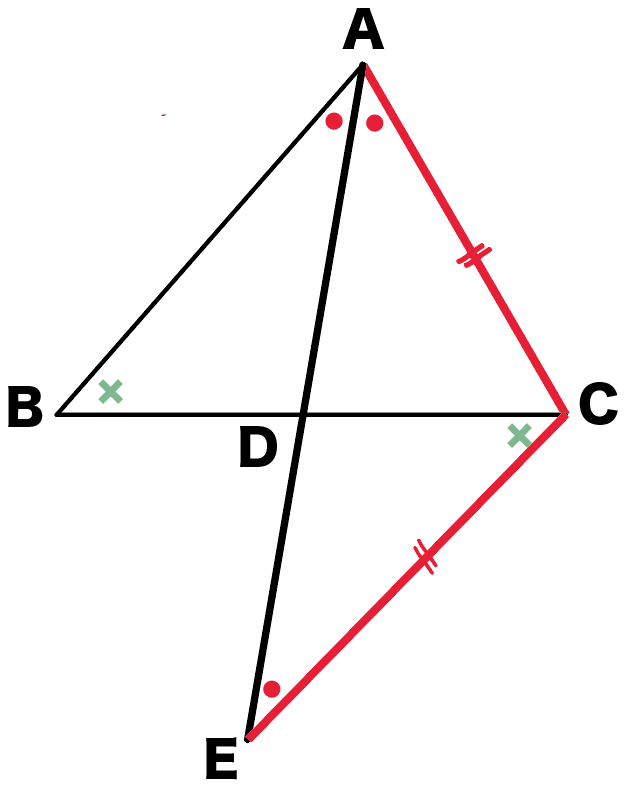
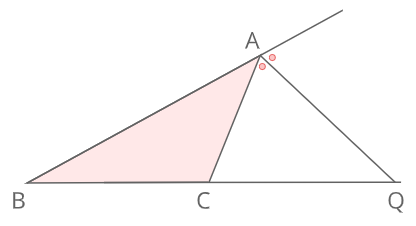
DC=e, AD=f DC = e,AD = f とおくとき以下の公式が成立する。 1:ae=bd 1:ae = bd 2: (ab)f=2ab\cos \dfrac {A} {2} 2:(a b)f = 2abcos 2A 3:f^2=abde 3:f 2 = ab−de 角の二等分線と垂線 – GeoGebra Materials まず、 AB = c 、 AC = b 、 AD = d とし、 AD は ∠ BAC の2等分線なので、補題より、 BD = a c b c 、 DC = a b b c です。 ここで A から辺 BC に垂線を下ろし、交点を E とします。 直角三角形 ABE について c 2 = A E 2 BMathAquarium定理・公式の証明三角形の角の二等分線と比 2 2 AB>AC である ABC の∠A の外角の二等分線と 直線BC の交点をQ とする。すなわち, ∠XAQ=∠CAQ のとき,次の等式が成り立つ。 AB:AC=BQ:CQ 証明 点C を通り直線AQ と平行な直線と,辺AB との



1




1 Adza 1 2 Descubre Como Resolverlo En Qanda
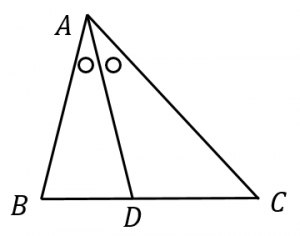
三角形の比角の二等分線の定理・性質の問題の解き方がわかる3ステップ 三角形の角の二等分線の定理をつかった問題わからん! こんにちは!この記事を書いてるKenだよ。ナンは1つでいいね。 三角形の角の二等分線の定理・性質 っておぼえてるかな? 三角形の内角の二等分線と比 △ABC の ∠A の二等分線は辺 BC を ABAC に内分する。知っておくと役に立つ以下の定理があります。 角の 2 2 等分と線分の比 下図のように、角 A A の 2 2 等分線と、 BC B C の交点を D D とします。 このとき、 BD DC = AB AC B D D C = A B A C 一応、中学数学の範囲外なので、頻繁に出題されるものではありませんが




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



三角形の角の二等分線の性質 定理の証明がわかる5ステップ Qikeru 学びを楽しくわかりやすく
角の二等分線とは、その名の通り、 ある角を二等分した線 のことです。 角を 内分 する「内角の二等分線」と、 外分 する「外角の二等分線」の 種類があります。 内角でも外角でも、 辺の比 は同じ関係式で表されます( 角の二等分線の定理 )。学校法人 福山暁の星学院 〒 広島県福山市西深津町三丁目4番1号 tel(学院直通) fax(学院直通) 今回の問題は「 角の二等分線と比 」です。 問題 次の図で、 で の内角の二等分線と直線 との交点を 、 の外角の二等分線と直線 との交点を とするとき、 の長さを求めよ。 次のページ「解法のPointと問題解説」 次へ 1 2 中点連結定理と平行線と比 三角



三角形の角の二等分線の性質 定理の証明がわかる5ステップ Qikeru 学びを楽しくわかりやすく



傍心 ぼうしん とは 東大合格コム
平行線と線分の比 平行線と線分の比 1 pq//bc ⇔ apab = aqac 2 pq//bc ⇔ appb = aqqc 3 pq//bc ⇒ apab = pqbc a p q p q a b c b c ※3だけ逆は成り立たない。 角の二等分線と比 角の二等分線と比 1 abcの∠aの二等分線と辺bcとの 交点pは辺bcをabbcに内分する。る、これらの証明は「角の二等分線」、l'相似比j、「三角形の面積」等 を用いてなされる。そして、これらの結果はq』学校・高等学院におけ る数学的活動の教材として用いることができると思われる。 キーワード: 傍接円、傍心、角の二等分線 1。①角の二等分線に平行な補助線CEを加えた図を示し,平行線と比の関係を用いて課題を解決することを説明する。 ・比の関係が等しい組はどれか考える。 BA:AEとBD:DC ・角の関係が等しい組はどれか考える。 ・課題の定理を証明する。




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext




内角と外角の二等分線の定理の忘れない覚え方 Youtube
三角形の角の二等分線の性質の証明がわかる5ステップ ゆうき先生 三角形の二等分線の定理の証明は、 補助線をひく 相似な図形をみつける 辺の比に注目する 二等辺三角形をさがす 証明をかく の5ステップだよ。オイラーの公式と角の二等分線 MathWills 角度を単位円上の点として扱う幾何代数の技法によって、角の二等分線の性質を確認します。 クリフォード代数は使用しないで、複素平面上でオイラーの公式に基づく計算を行います。 ※ 図は Markdown に SVG を直接命題3231 内角の二等分線 三角形の内角の二等分線は対辺をその角を挟む二辺と同じ比に内分する。すなわち、三角形 abo において、角 o の二等分線と対辺の交点を c とすれば、 oa ob = ac cb が成




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



三角形の角の二等分線と比
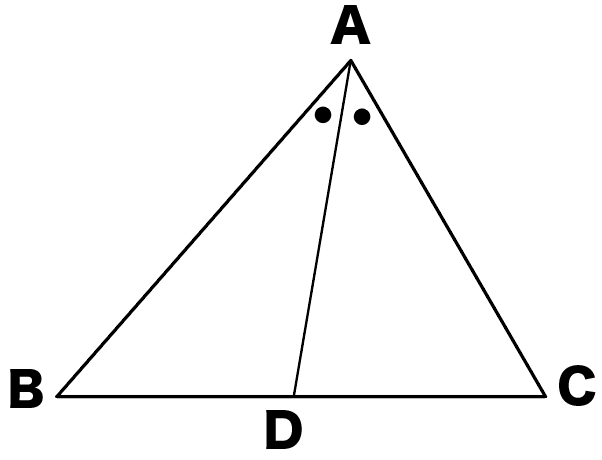
二等辺三角形は2つの辺の長さが等しいことで、上のような性質が出てきます。これらの性質がそれぞれ正しいことを確認してみましょう。今回はその2つ目の性質の 頂角の二等分線は、底辺を垂直に二等分する こと確認していきたいと思います。 参考:二等辺三角形の1つ目の性質「2つの角は特に、二等辺三角形のとき、ピタゴラスの定理が成り立つ。 「ピタゴラスの定理」「余弦定理」「トレミーの定理」「角の二等分線定理」「中線定理」など幾 何的な証明がありますが、これらをそれぞれ直接に代数的に証明できるのではないでしょう か?三角形の角の二等分線と辺の比 三角形ABCにおいて、∠BACを二等分する線とBCとの交点をDとしたとき、次の定理が成り立つ。 このテキストでは、この定理を証明します。 証明 図のように、∠BACの二等分線と辺BCとの交点をDと




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
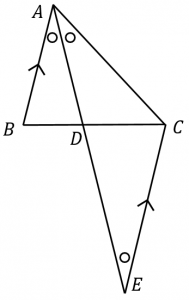



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学
Page 1 高校で教えたい幾何の問題 角の二等分線の性質を狩る 札幌旭丘高校 中村文則 はじめに 三角形ABC の頂角Aの二等分線を,正確に引けない生徒が意外と多いことに驚く. 辺BC の中点と交わり、なぜか中線になってしまう.「角の二等分」から「辺の二等分」へと安易に結び三角形の角の二等分線と比 三角形の角の二等分線と比には以下の定理がある。 \(\triangle{ABC}\)の\( \angle A\)の二等分線と辺BCとの交点Pは、辺BCをABACに内分する。 \( AB \ne AC \)である\( \triangle{ABC} \)の頂点Aにおける外角の二等分線と辺BCの延長との交点Qは、辺BCを 二等辺三角形とは?定義 二等辺三角形とは、 \(\bf{2}\) つの辺の長さが等しい三角形 のことです。 二等辺三角形の等しい \(2\) 辺の間の角のことを「頂角」、その他の \(2\) つの角のことを「底角」といいます。そして、頂角に向かい合う辺のことを「底辺」といいます。



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su




角の二等分線と比 おいしい数学
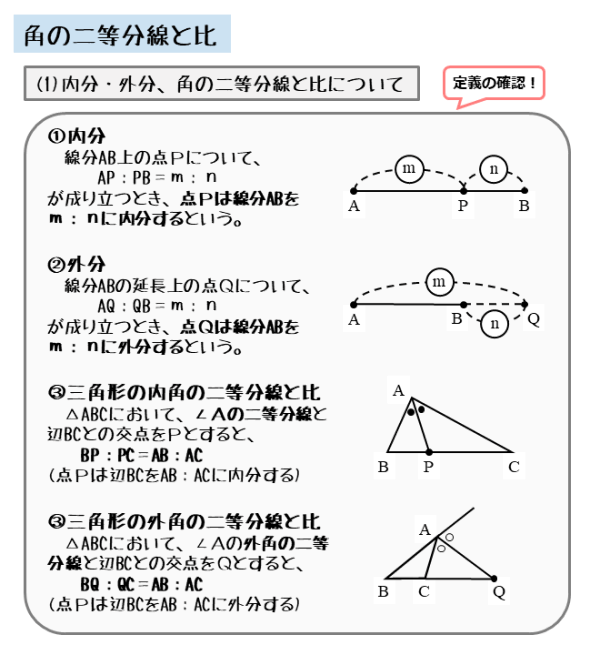



図形の性質 角の二等分線と比について 日々是鍛錬 ひびこれたんれん



三角形の角の二等分線と比
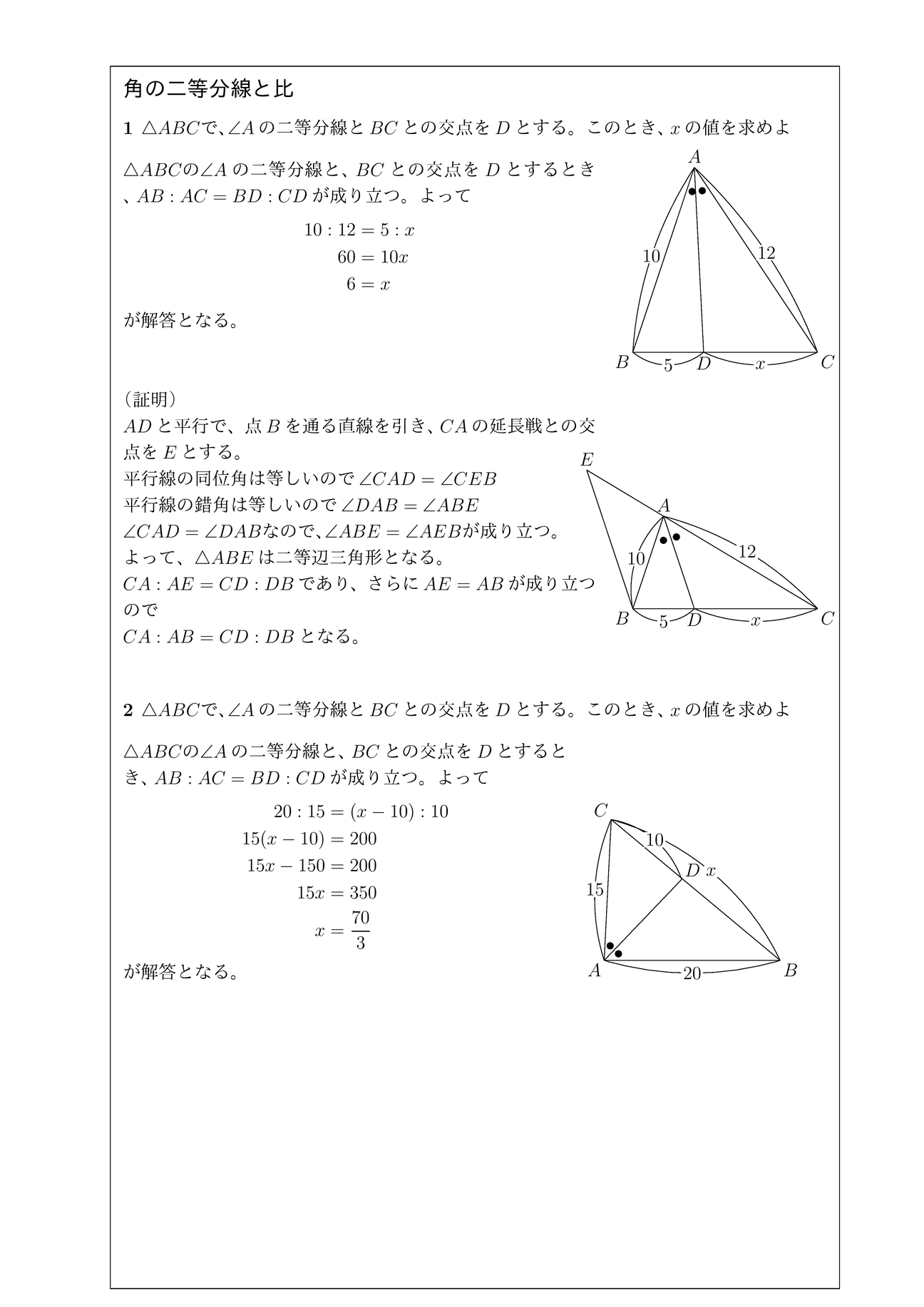



角の二等分線と比 チーム エン




内角の二等分線 外角の二等分線の比の定理 証明 Youtube



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア




三角形の問題 平行 二等辺三角形 問題 三角形abcにおいて 角bの二 Okwave




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



Math 平行と合同 角の二等分線と角度 働きアリ




角の二等分線の長さを導出する4通りの方法 理系のための備忘録




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ



三角形の角の二等分線と比1 Geogebra
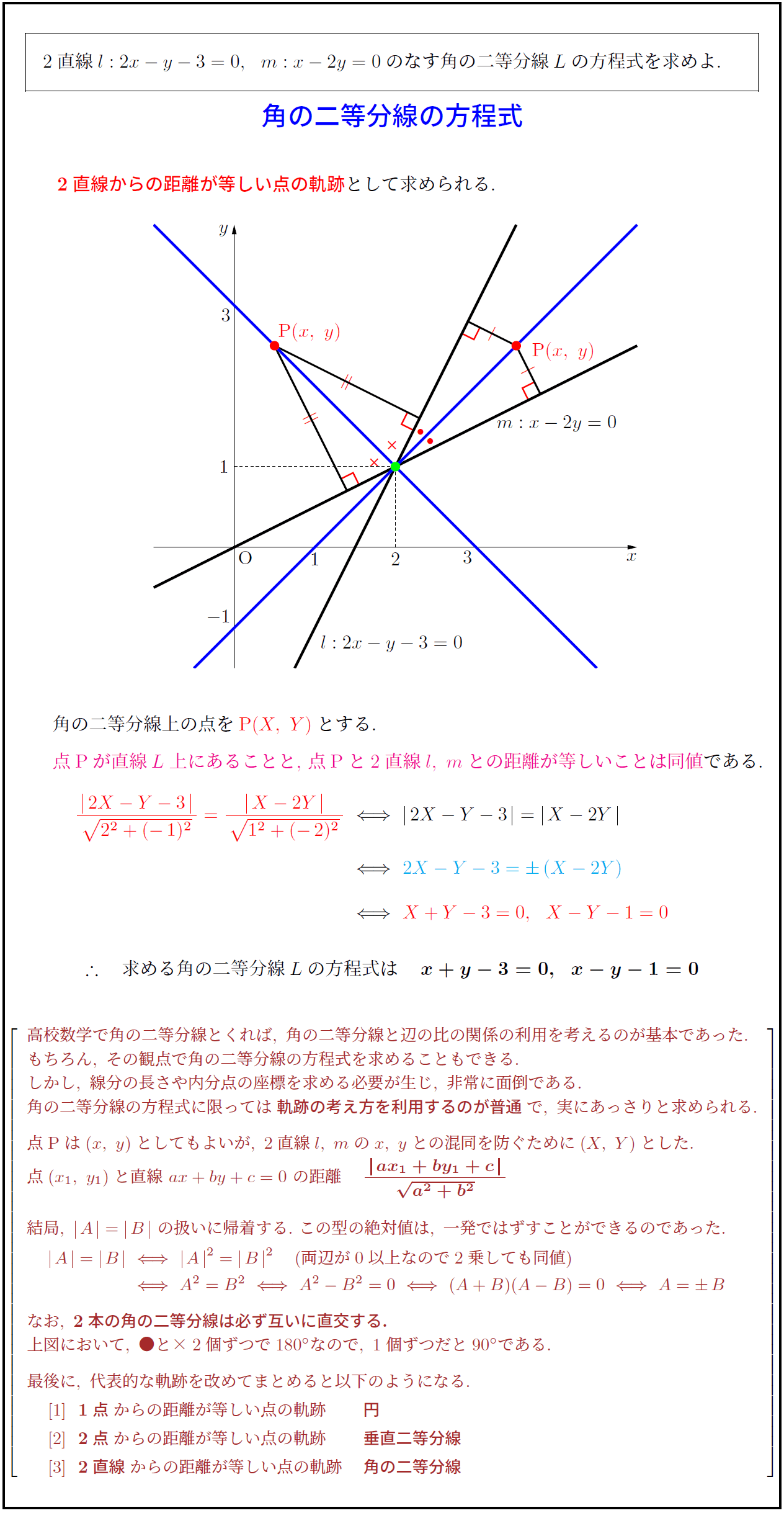



高校数学 角の二等分線の方程式 軌跡の利用 受験の月



中学3年生の相似な図形 角の二等分線と比に関する問題です 以下の写真 Yahoo 知恵袋




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ
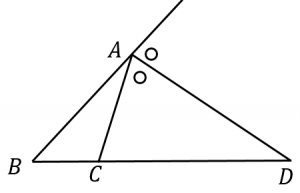



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学



三角形の角の二等分線と比



Q Tbn And9gcrd P2pctuz8gfkpppw9apzd Qqafrxhfweennrb5u0gatejnzy Usqp Cau




サクッと解説 角の二等分線と比の特徴となぜ について 数スタ



1



内接円 内心




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




発展 三角比と角の二等分線 なかけんの数学ノート
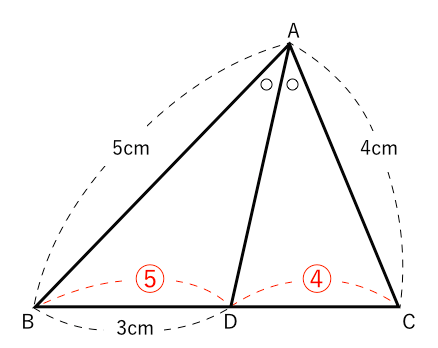



相似な図形 角の二等分があったらこれ 苦手な数学を簡単に



三角形の内角の二等分線 メネラウスの定理 チェバの定理



角の二等分線に関する重要な3つの公式 高校数学の美しい物語




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext




高校数学a 外角の二等分線と比 練習編 映像授業のtry It トライイット




高校数学a 角の二等分線と比の利用 例題編 映像授業のtry It トライイット



三角形の角の二等分線の性質 定理の証明がわかる5ステップ Qikeru 学びを楽しくわかりやすく



三角形の角の二等分線の性質 定理の証明がわかる5ステップ Qikeru 学びを楽しくわかりやすく




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




角の二等分線と比 おいしい数学
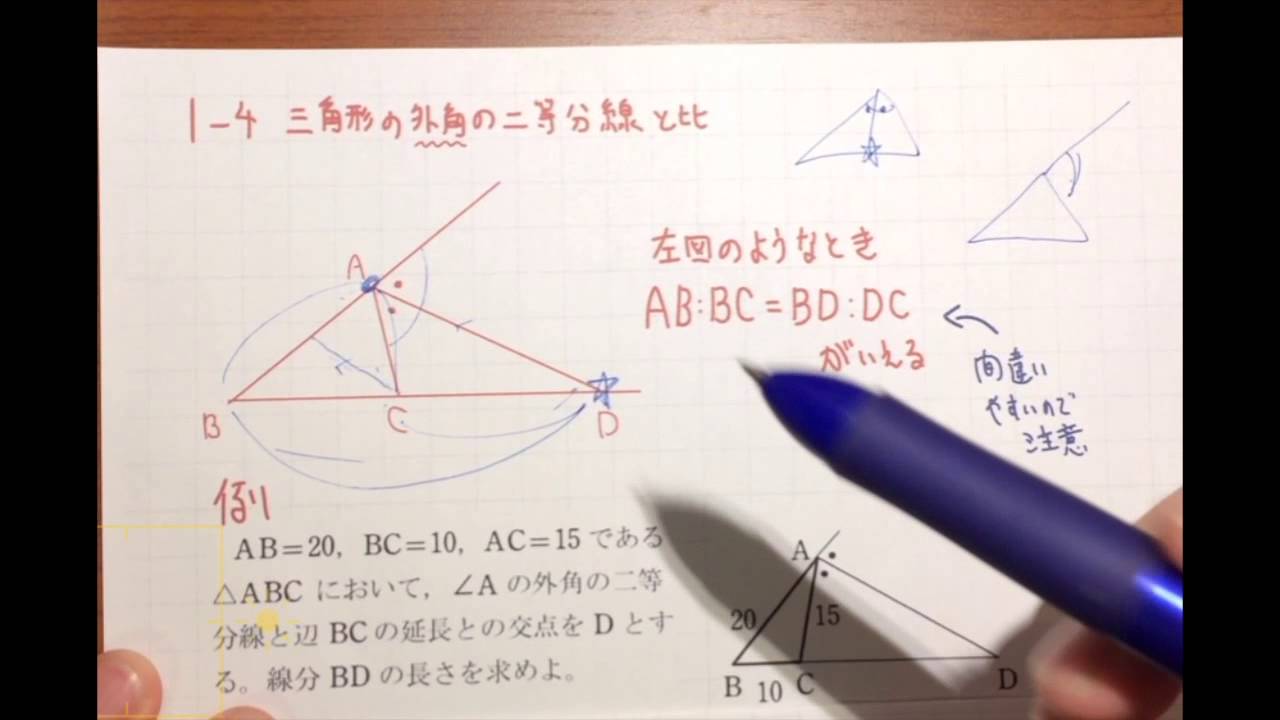



三角形の外角の二等分線と比 Youtube



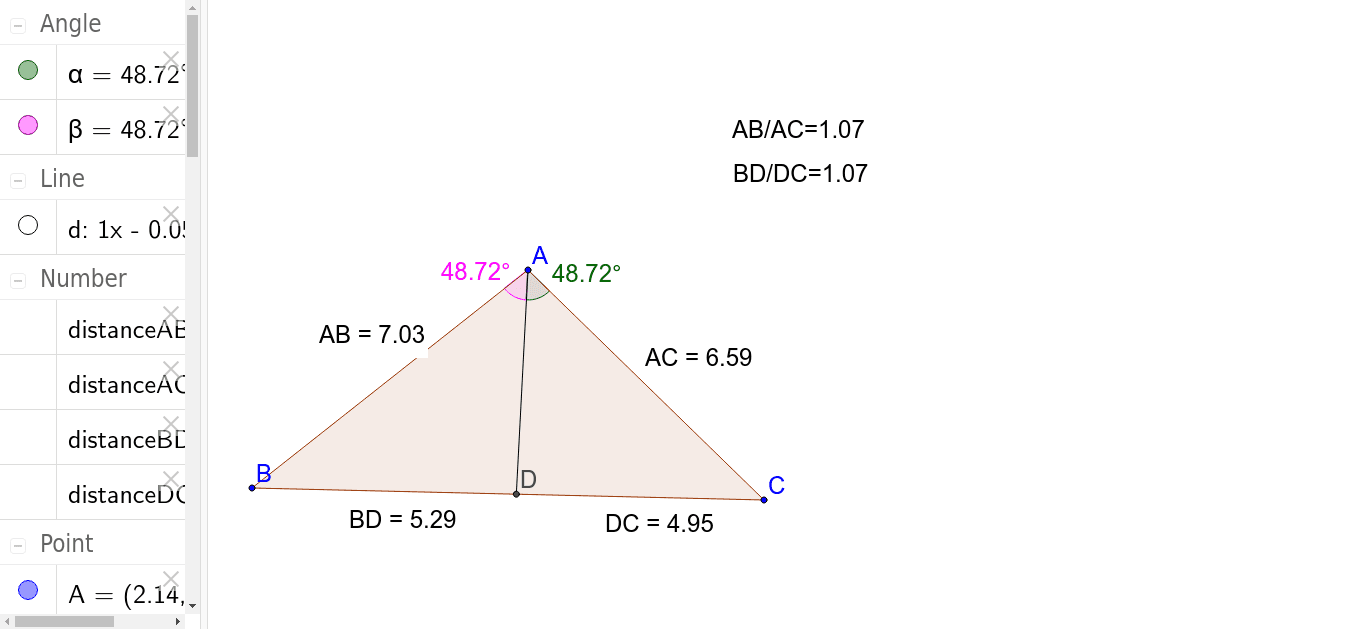
三角形の角の二等分線と比の定理 Geogebra




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ




中学数学 裏技 三角形の角の二等分線の長さを求める下書き やはり俺の考察ブログはまちがっている アニメ 数学




図形の性質 角の二等分線と比について 日々是鍛錬 ひびこれたんれん



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



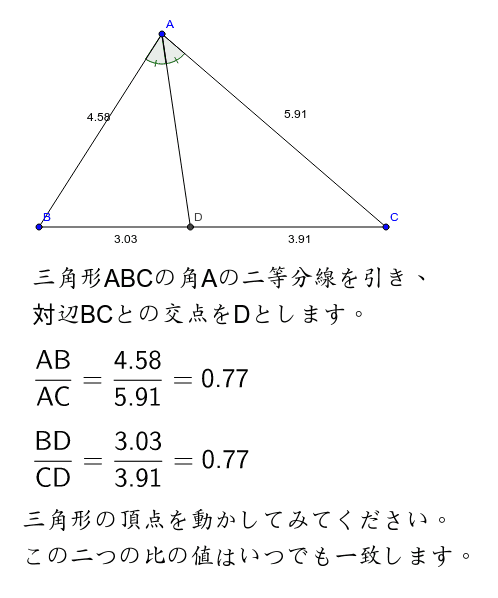
三角形の角の二等分線と比 Geogebra



受験数学かずスクール 三角形の角の二等分線の定理の解説 図形的な意味は面積の比




三角形の面積 応用 角の二等分線 Youtube



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



中3数学 角の二等分線定理のポイントと練習問題




基本 三角比と角の二等分線 なかけんの数学ノート



傍接円 傍心について



三角形の内角の2等分線と対辺 Geogebra




頂角の二等分線が底辺を分割するときの比に関する問題 大垣日大高校入試問題より 身勝手な主張




中3 19 1三角形の角の二等分線と線分比 Youtube
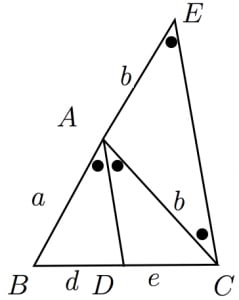



角の二等分線に関する重要な3つの公式 高校数学の美しい物語




角の2等分線によって分ける比 身勝手な主張
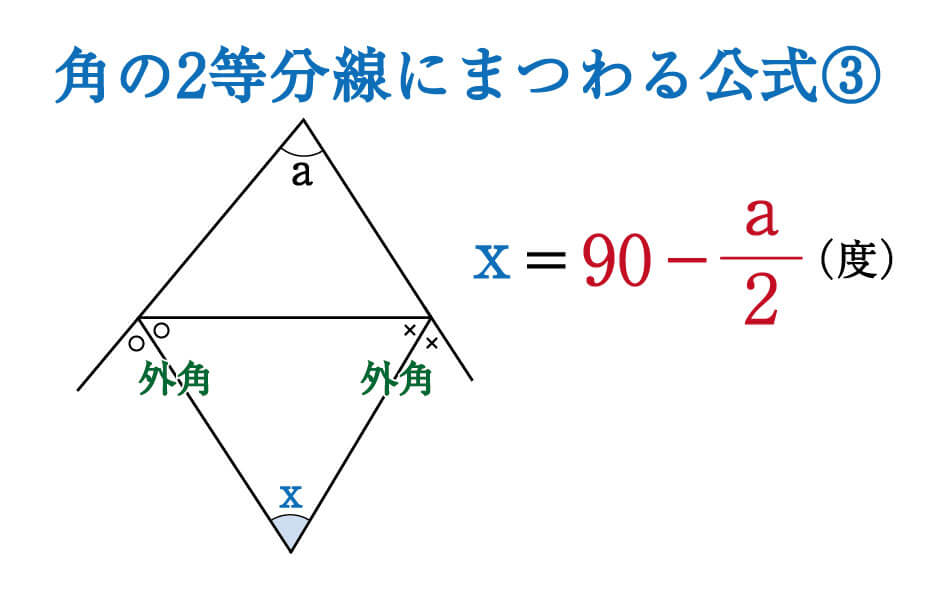



数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




高校数学 数 98 三角形の内角の二等分線 Youtube




角の二等分線の長さ の公式の証明 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学b 角の二等分線のベクトル2パターン 受験の月




高校数学a 角の二等分線と比の利用 練習編 映像授業のtry It トライイット




中学数学 角の二等分線定理の高校入試対策問題 Pikuu
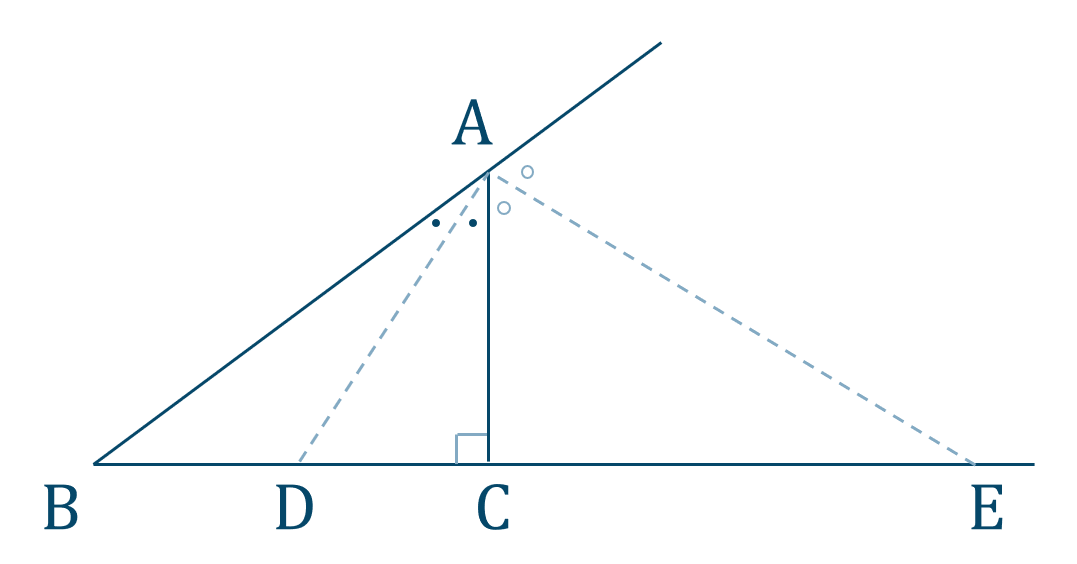



数学a 角の二等分線と比の使い方とコツ 教科書より詳しい高校数学



三角形の角の二等分線定理




勉強しよう数学 角の二等分線の長さ 相似図形による定理の証明



算数 基本 角の二等分線の性質 まいにち一題 中学受験過去問題研究




角の二等分線に関する問題 一目瞭然早見チャート 高校生 数学のノート Clear




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学
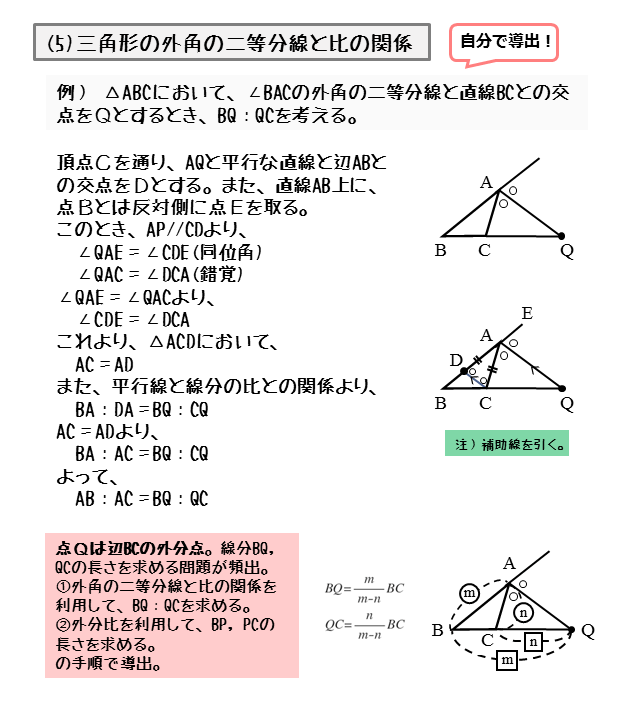



図形の性質 角の二等分線と比について 日々是鍛錬 ひびこれたんれん
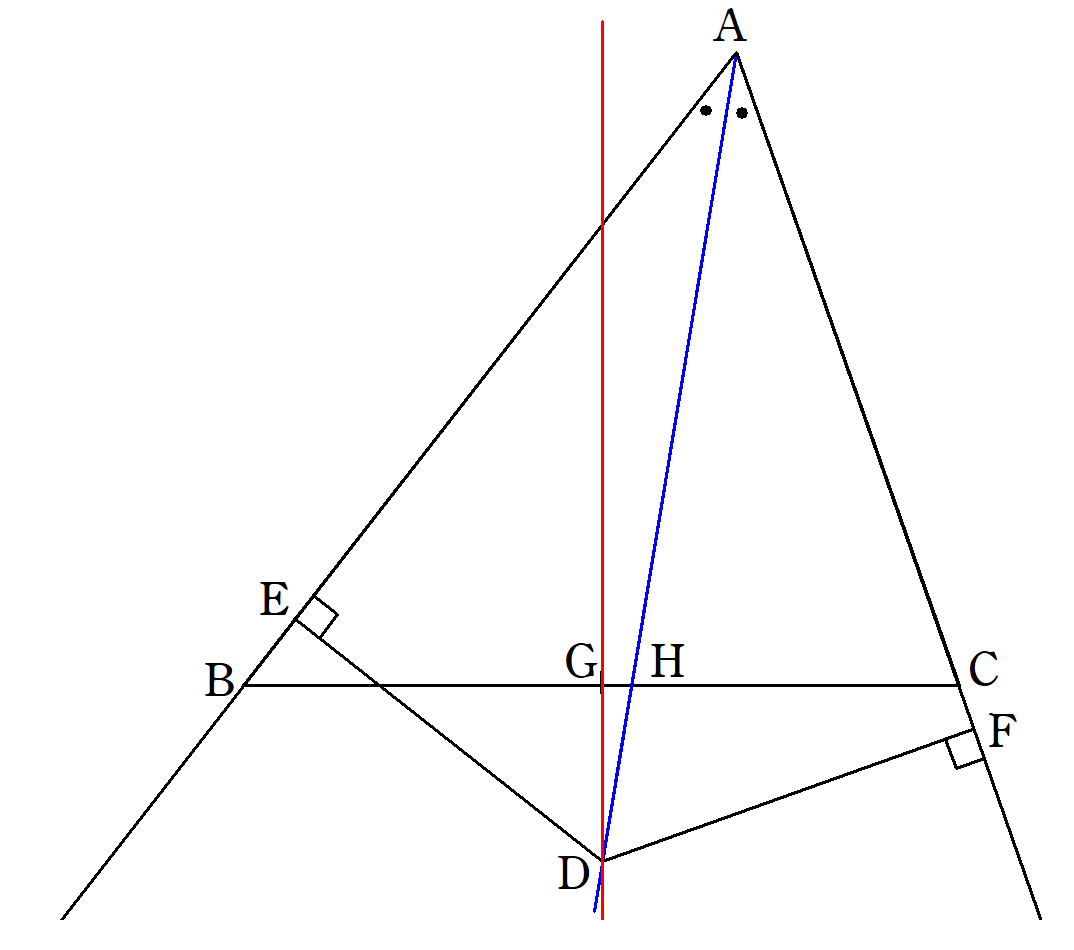



二等分線と垂線の定理 Fukusukeの数学めも




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学
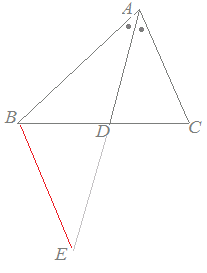



角の二等分線と補助線



高校入試数学 面積比のポイントと練習問題




三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア




高校数学a 外角の二等分線と比 練習編 映像授業のtry It トライイット
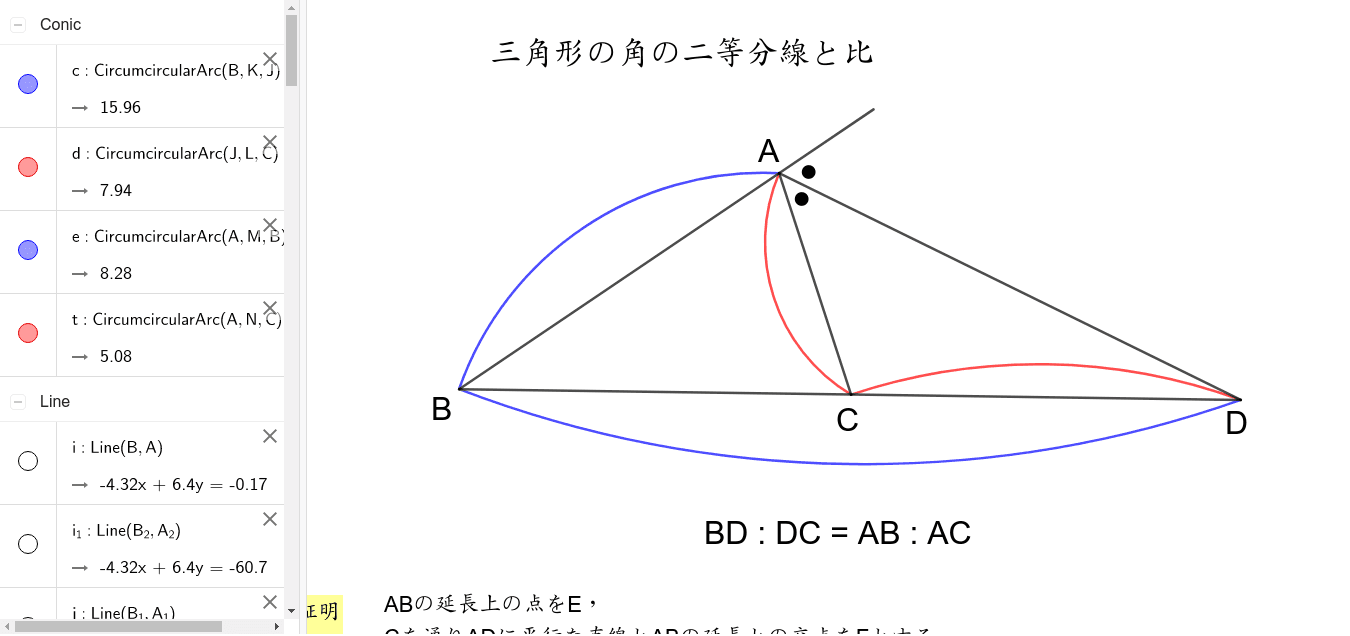



三角形の角の二等分線と比2 Geogebra
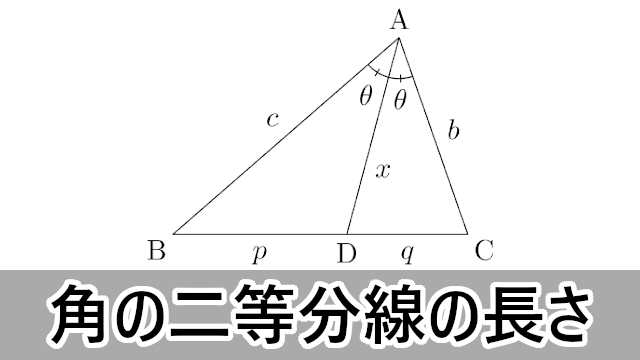



数学ia 三角形の内角の二等分線の長さ 大学入試数学の考え方と解法



三角形の角の二等分線 大学受験の王道



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ
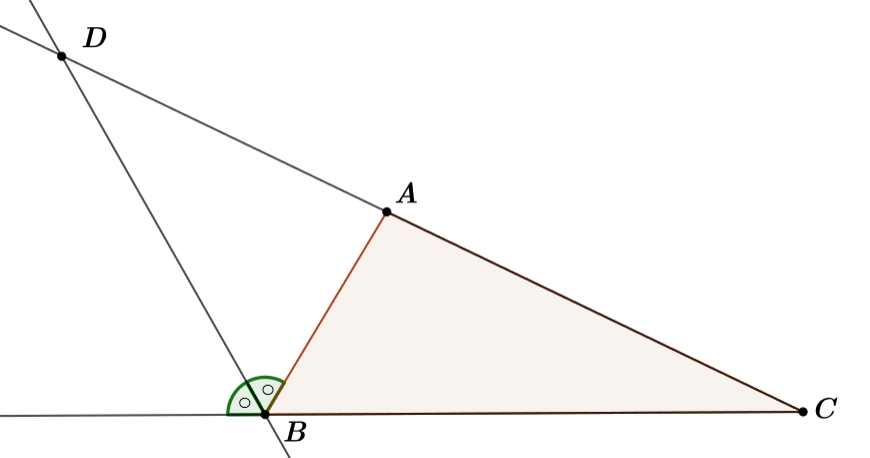



内角の二等分線と外角の二等分線 内は外で外は内 キソカラ



三角形の角の二等分線定理 外角



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



高校数学 外角の二等分線と比 の公式とその証明 Enggy



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学



48s96ub7b0z5f Net Bekutoru Nitoubunsen




頂角の二等分線は底辺を二等分する Youtube




二等辺三角形の性質の証明 頂角の二等分線 Youtube




数学aの三角形の角の二等分線と比の問題についてです 1からさっぱりわ 数学 教えて Goo



数a三角形の角の二等分線と比について Dc Ab A Yahoo 知恵袋



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典



0 件のコメント:
コメントを投稿